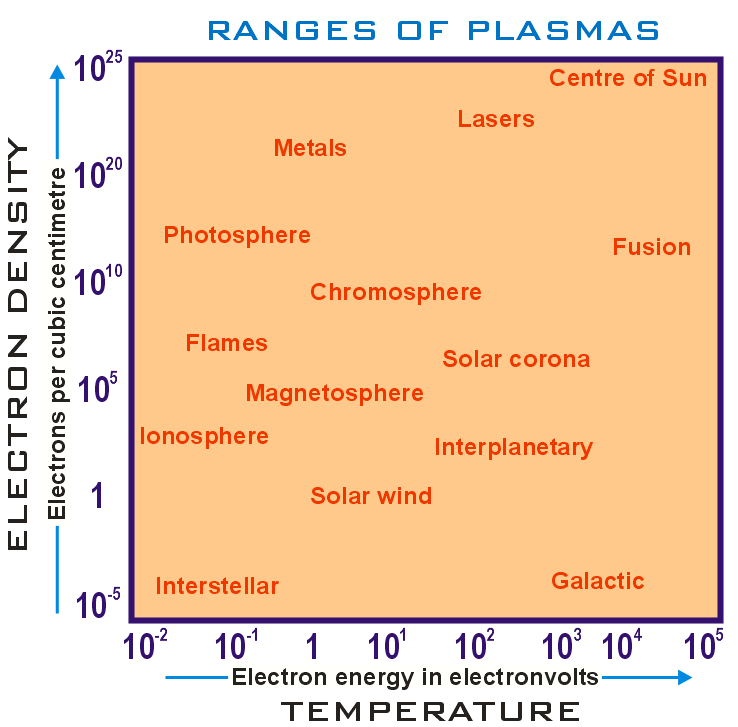
The parameters of plasmas, including their spatial and temporal extent, vary by many orders of magnitude. Nevertheless, there are significant similarities in the behaviors of apparently disparate plasmas. It is not only of theoretical interest to understand the scaling of plasma behavior, it also allows the results of laboratory experiments to be applied to larger natural or artificial plasmas of interest. The situation is similar to testing aircraft or studying natural turbulent flow in wind tunnels.
Similarity transformations (also called similarity laws) help us work out how plasma properties changes in order to retain the same characteristics. A necessary first step is to express the laws governing the system in a nondimensional form. The choice of nondimensional parameters is never unique, and it is usually only possible to achieve by choosing to ignore certain aspects of the system.
One dimensionless parameter characterizing a plasma is the ratio of ion to electron mass. Since this number is large, at least 1836, it is commonly taken to be infinite in theoretical analyses, that is, either the electrons are assumed to be massless or the ions are assumed to be infinitely massive. In numerical studies the opposite problem often appears. The computation time would be intractably large if a realistic mass ratio were used, so an artificially small but still rather large value, for example 100, is substituted. To analyze some phenomena, such as lower hybrid oscillations, it is essential to use the proper value.
A commonly used similarity transformation

Hannes Alfvén suggested that, by scaling laboratory results by a factor of 109, he could extrapolate magnetospheric conditions. Another scaling jump of 109 was required to extrapolate to galactic conditions, and a third jump of 109 was required to extrapolate to the Hubble distance [2]
One commonly used similarity transformation was derived for gas discharges by James Dillon Cobine (1941)[3], Alfred Hans von Engel and Max Steenbeck (1934)[4], and further applied by Hannes Alfvén and Carl-Gunne Fälthammar to plasmas.[5] They can be summarised as follows:
Similarity Transformations Applied to Gaseous Discharges and some Plasmas
| Property | Scale Factor | |
|---|---|---|
| length, time, inductance, capacitance | x1 | x |
| particle energy, velocity, potential, current, resistance | x0=1 | Unchanged |
| electric and magnetic fields, conductivity, neutral gas density, ionization fraction | x-1 | 1/x |
| current density, electron and ion densities | x-2 | 1/x2 |
This scaling applies best to plasmas with a relatively low degree of ionization. In such plasmas, the ionization energy of the neutral atoms is an important parameter and establishes an absolute energy scale, which explains many of the scalings in the table:
- Since the masses of electrons and ions cannot be varied, the velocities of the particles are also fixed, as is the speed of sound.
- If velocities are constant, then time scales must be directly proportional to distance scales.
- In order that charged particles falling through an electric potential gain the same energy, the potentials must be invariant, implying that the electric field scales inversely with the distance.
- Assuming that the magnitude of the E-cross-B drift is important and should be invariant, the magnetic field must scale like the electric field, namely inversely with the size. This is also the scaling required by Faraday’s law of induction and Ampère’s law.
- Assuming that the speed of the Alfvén wave is important and must remain invariant, the ion density (and with it the electron density) must scale with B2, that is, inversely with the square of the size. Considering that the temperature is fixed, this also ensures that the ratio of thermal to magnetic energy, known as beta, remains constant. Furthermore, in regions where quasineutrality is violated, this scaling is required by Gauss’s law.
- Ampère’s law also requires that current density scales inversely with the square of the size, and therefore that current itself is invariant.
- The electrical conductivity is current density divided by electric field and thus scales inversely with the length.
- In a partially ionized plasma, the electrical conductivity is proportional to the electron density and inversely proportional to the neutral gas density, implying that the neutral density must scale inversely with the length, and ionization fraction scales inversely with the length.
Limitations
While these similarity transformations capture some basic properties of plasmas, not all plasma phenomena scale in this way. Consider, for example, the degree of ionization, which is dimensionless and thus would ideally remain unchanged when the system is scaled. The number of charged particles per unit volume is proportional to the current density, which scales as x -2, whereas the number of neutral particles per unit volume scales as x -1 in this transformation, so the degree of ionization does not remain unchanged but scales as x -1.
Astrophysical application
As an example, take an auroral sheet with a thickness of 1 km. A laboratory simulation might have a thickness of 10 cm, a factor of 104 smaller. To satisfy the condition of this similarity transformation, the gaseous density would have to be increased by a factor of 104 from 104 m-3 to 108 m-3 (1010 cm-3 to 1014 cm-3), and the magnetic field would have to be increased by the same factor from 50 microteslas to 500 milliteslas (0.5 gauss to 5 kilogauss). These values are large but within the range of technology. If the experiment captures the essential features of the aurora, the processes will be 104 times faster so that a pulse that takes 100 s in nature would take only 10 ms in the laboratory.
Similarity transformations applied to some astrophysical plasmas
Actual plasma properties compared to a laboratory plasma if the scale length is reduced to 10 cm.
| Region | Characteristic dimension (cm) | Density (particles/cm3) | Magnetic field (gauss) | Characteristic time | |||||
| Actual | Scaled | Scale Factor | Actual | Scaled | Actual | Scaled | Actual | Scaled | |
| Ionosphere | 106 – 107 | 10 | 10-5 – 10-6 | 1010 | 1015 – 1016 | 0.5 | 5×104 – 5×105 | Period of Giant pulsation | |
| 100 s | 0.1 – 1 ms | ||||||||
| Exosphere | 109 | 10 | 10-8 | 105 – 10 | 1013 – 109 | 0.5 – 5×10-4 | 5×107 – 5×104 | One Day | |
| 105 s | 1 ms | ||||||||
| Interplanetary space | 1013 | 10 | 10-12 | 1 – 10 | 1012 – 1013 | 10-4 | 108 | One Solar Rotation | |
| 2×106 s | 2 μs | ||||||||
| Interstellar space | 3×1022 | 10 | 3×10-22 | 1 | 3×1021 | 10-6 – 10-5 | 3×1015 – 3×1016 | Period of galactic rotation | |
| 1×1016 s | 3 μs | ||||||||
| Intergalactic space | >3×1027 | 10 | <3×10-27 | 10-4? | >3×1022 | 10-7? | >3×1019 | Age of the Universe | |
| 4×1017s | 1×10-9s | ||||||||
| Solar chromosphere | 108 | 10 | 10-7 | 1011 – 1014 | 1018 – 1021 | 103 – 1 | 1010 – 107 | Life of Solar Flare | |
| 103 s | 100 μs | ||||||||
| Life of Solar Prominence | |||||||||
| 105 s | 10 ms | ||||||||
| Solar corona | 1010 – 1011 | 10 | 10-9 – 10-10 | 108 – 106 | 1017 – 1016 | 102 – 10-1 | 1011 – 109 | Life of Coronal Arc | |
| 103 s | 10-1 to 1 µs | ||||||||
| Solar Cycle | |||||||||
| 22 years | 70 to 700 ms | ||||||||
Particle density of the Earth’s atmosphere at sea level is 1019 per cm3
Small bar magnet = 100 milliteslas. Big electromagnet = 2 teslas
109 cm = 10,000 km
The table shows the properties of some actual space plasma (see the columns labelled Actual). It also shows how other plasma properties would need to be changed, if (a) the characteristic length of a plasma were reduced to just 10 cm, and (b) the characteristics of the plasma were to remain unchanged.
The first thing to notice is that many cosmic phenomena cannot be reproduced in the laboratory because the necessary magnetic field strength is beyond the technological limits. Of the phenomena listed, only the ionosphere and the exosphere can be scaled to laboratory size. Another problem is the ionization fraction. When the size is varied over many orders of magnitude, the assumption of a partially ionized plasma may be violated in the simulation. A final observation is that the plasma densities needed in the laboratory are sizeable, up to 1016 cm-3 for the ionosphere, compared to the atmospheric density of about 1019 particles per cm3. In other words, the laboratory analogy of a low density space plasma is not a “vacuum chamber”, but laboratory plasma with a pressure, when the higher temperature is taken into consideration, which can approach atmospheric pressure.
Notes
- ↑ After Peratt, A. L., “Advances in Numerical Modeling of Astrophysical and Space Plasmas” (1996) Astrophysics and Space Science, v. 242, Issue 1/2, p. 93-163. FULL TEXT PEER REVIEWED
- ↑ Hannes Alfvén, “On hierarchical cosmology” FULL TEXT (1983) Astrophysics and Space Science (ISSN 0004-640X), vol. 89, no. 2, Jan. 1983, p. 313-324. PEER REVIEWED
- ↑ Cobine, J. D ., 1941: Gaseous Conductors, McGraw-Hill . New York. ACADEMIC BOOK
- ↑ von Engel, A., and Steenbeck, M., 1934: ElektrischeGasentladungen, Springer-Verlag, Berlin. See also von Engel, 1955: Ionized Gases, Clarendon Press, Oxford.
- ↑ H. Alfvén and C.-G. Falthammar, Cosmic electrodynamics (2nd Edition, Clarendon press, Oxford, 1963) See 4.2.2. Similarity Transformations. ACADEMIC BOOK
References
- Peratt, A. L., “Advances in Numerical Modeling of Astrophysical and Space Plasmas” (1996) Astrophysics and Space Science, v. 242, Issue 1/2, p. 93-163. FULL TEXT PEER REVIEWED
- Peratt, Anthony L., “Advances in Numerical Modeling of Astrophysical and Space Plasmas“, Astrophysics and Space Science, v. 256, Issue 1/2, p. 51-75 (1997) Paper FULL TEXT PDF PEER REVIEWED