Double layer

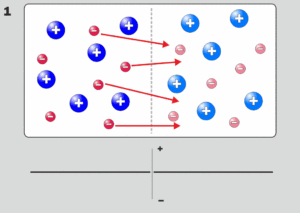
A double layer is a structure in a plasma and consists of two parallel layers with opposite electrical charge. The sheets of charge cause a strong electric field and a correspondingly sharp change in voltage (electrical potential) across the double layer. Ions and electrons which enter the double layer are accelerated, decelerated, or reflected by the electric field. In general, double layers (which may be curved rather than flat) separate regions of plasma with quite different characteristics. Double layers are found in a wide variety of plasmas, from discharge tubes to space plasmas to the Birkeland currents supplying the Earth’s aurora, and are especially common in current-carrying plasmas. Compared to the sizes of the plasmas which contain them, double layers are very thin (typically ten Debye lengths), with widths ranging from a few millimeters for laboratory plasmas to thousands of kilometres for astrophysical plasmas.

Other names for a double layer are: electrostatic double layer, electric double layer, plasma double layers, electrostatic shock (a type of double layer which is oriented at an oblique angle to the magnetic field in such a way that the perpendicular electric field is much larger than the parallel electric field),^[6] space charge layer,^[7] and “potential ramp”.^[8] In laser physics, a double layer is sometimes called an ambipolar electric field.^[9] Double layers are conceptually related to the concept of a ‘sheath’ (see Debye sheath).

The adopted electrical symbol for a double layer, when represented in an electrical circuit is:
────DL────
If there is a net current present, then the DL is oriented so that the base of the L is in line with direction of current.^[10]

An overview of double layers in space, experiment and simulation is given in the introduction of ref. ^[11]

Double layer classification

Double layers may be classified in the following ways:

• Weak and strong double layers. The strength of a double layer is expressed as the ratio of the potential drop in comparison with the plasma’s equivalent thermal potential, or in comparison with the rest mass energy of the electrons. A double layer is said to be strong if the potential drop across the layer is greater than the equivalent thermal potential of the plasma’s components. This means that for strong double layers there are four different components to the plasma: 1. the electrons entering at the low potential side of the double layer which are accelerated; 2. the ions entering at the high potential side of the double layer which are accelerated; 3. the electrons entering at the high potential side of the double layer which are decelerated and successively refelected; and 4. the ions which enter the double layer at the low potential side of the double layer which are decelerated and reflected. Note that in the case of a weak double layer, the electrons and ions entering from the “wrong” side are decelerated by the electric field, however most will not be reflected, as the potential drop is not strong enough.
• Relativistic or nonrelativistic double layers. A double layer is said to be relativistic if the potential drop over the layer is so large that the total gain in energy of the particles is larger than the rest mass energy of the electron. The charge distribution in a relativistic double layer is such that the charge density is located in two very thin layers, and inside the double layer the density is constant at and very low compared to the rest of the plasma. In this respect, the double layer is similar to the charge distribution in a capacitor. As a special case of a relativistic double layer one can consider the vacuum gap at the magnetic polar cap of a pulsar.
• Current carrying and current-free double layers may both occur. Current carrying double layers may be generated by current-driven plasma instabilities which amplify variations of the plasma density. Current-free double layers form on the interface between two plasma regions with different characteristics, and their associated electric field maintains a balance between the penetration of electrons in either direction (so that the net current is low).

Double layer formation

 

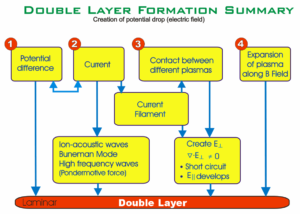
There are two different kinds of double layers, which are formed differently:

Current carrying double layers

Current carrying double layers may arise in plasmas carrying a current. Various instabilities can be responsible for the formation of these layers. One example is the Buneman instability which occurs when the streaming velocity of the electrons (basically the current density divided by the electron density) exceeds the electron thermal velocity of the plasma. Double layers (and other phase space structures) are often formed in the non-linear phase of the instability. One way of viewing the Buneman instability is to describe what happens when the current (in the form of a zero temperature electron beam) has to pass through a region of decreased ion density. In order to prevent charge from accumulating, the current in the system must be the same everywhere (in this 1D model). The electron density also has to be close to the ion density (quasineutrality), so there is also a dip in electron density. The electrons must therefore be accelerated into the density cavity, to maintain the same current density with a lower density of charge carriers. This implies that the density cavity is at a high electrical potential. As a consequence, the ions are accelerated out of the cavity, amplifying the density perturbation. Then there is the situation of a double-double layer, of which one side will most likely be convected away by the plasma, leaving a regular double layer. This is the process in which double layers are produced along planetary magnetic field lines in so-called Birkeland currents.

Current-free double layers

Current-free double layers occur at the boundary between plasma regions with different plasma properties. We explain how they form (neglecting the ions which are considered solely as a neutralizing background). Consider a plasma divided into two regions by a plane, which has a higher electron temperature on one side than on the other (the same analysis can also be done for different densities). This means that the electrons on one side of the interface have a greater thermal velocity. The electrons may stream freely in either direction, and the flux of electrons from the hot plasma to the cold plasma will be greater than the flux of the electrons from the cold plasma to the hot plasma, because the electrons from the hot side have a greater average speed. Because many more electrons enter the cold plasma than exit it, part of the cold region becomes negatively charged. The hot plasma, conversely, becomes positively charged. Therefore, an electric field builds up, which starts to accelerate electrons towards the hot region, reducing the net flux. In the end, the electric field builds up until the fluxes of electrons in either direction are equal, and further charge build up in the two plasmas is prevented. The potential drop is in fact exactly equal to the difference in thermal potential between the two plasma regions in this case, so such a double layer is a marginally strong double layer.

Double layer formation mechanisms

The details of the formation mechanism depend on the environment of the plasma (eg. double layers in the laboratory, ionosphere, space plasmas, fusions plasma, etc). Proposed mechanisms for their formation have included:

• 1971: Between plasmas of different temperatures^[18]
• 1976: In laboratory plasmas^[19]
• 1982: Disruption of a neutral current sheet^[20]
• 1983: Injection of non-neutral electron current into a cold plasma^[21]
• 1985: Increasing the current density in a plasma^[22]
• 1986: In the accretion column of a neutron star^[23]
• 1986: By pinches in cosmic plasma regions ^[24]
• 1987: In a plasma constrained by a magnetic mirror^[25]
• 1988: By an electrical discharge^[26]
• 1988: Current-driven instabilities (strong double layers)^[27]
• 1988: Spacecraft-ejected electron beams^[28]
• 1989: From shock waves in a plasma^[29]
• 2000: Laser radiation^[30]
• 2002: When magnetic field-aligned currents encounter density cavities^[31]
• 2003: By the incidence of plasma on the dark side of the Moon’s surface^[32]

Features and characteristics of double layers

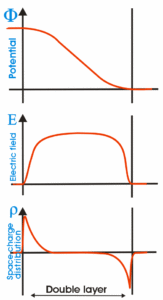
• Thickness: The production of a double layer requires regions with a significant excess of positive or negative charge, that is, where quasi-neutrality is violated.^[33][34] In general, quasi-neutrality can only be violated on scales of the order of the Debye length. The thickness of a double layer is of the order of ten Debye lengths, which is a few centimeters in the ionosphere, a few tens of meters in the interplanetary medium, and tens of kilometers in the intergalactic medium.
• Particle acceleration: The potential drop across the double layer will accelerate electrons and positive ions in opposite directions. The magnitude of the potential drop determines the acceleration of the charged particles. In strong double layers, this will result in beams or jets of charged particles.
• Particle populations: As described in the formation of double layers, there are four populations of charge particles inside a double layer (1) Free electrons that are accelerated across the double layer (2) Free positive ions that are accelerated in the opposite direction across the double layer (3) Reflected electrons that approach the double layer, but are reflected back and counter stream away (4) Reflected positive ions that approach the double layer, but are reflected back and counter stream away. Note that in the case of weak double layers not all electrons and ions entering “from the wrong side” will be reflected, and therefore there will also be a population of decelerated electrons and ions.

• Particle flux: For non-relativistic current carrying double layers the electrons comprise the main part of the particle flux. The Langmuir condition states that the ratio of the electron and the ion current across the layer is given by the square root of the mass ratio of the ions to the electrons.^[35] For relativistic double layers the current ratio is 1, i.e. equal amounts of current are carried by the electrons and the ions.
• Energy supply: In a certain limit, the voltage drop across a current-carrying double layer is proportional to the total current, and it might be thought of as a resistive element (or load) which absorbs energy in an electric circuit. Anthony Peratt (1991) wrote: “Since the double layer acts as a load, there has to be an external source maintaining the potential difference and driving the current. In the laboratory this source is usually an electrical power supply, whereas in space it may be the magnetic energy stored in an extended current system, which responds to a change in current with an inductive voltage”.^[36]
• Stability: Double layers in laboratory plasmas may be stable or unstable depending on the parameter regime.^[37] Various types of instabilities may occur, often arising due to the formation of beams of ions and electrons. Unstable double layers are noisy in the sense that they produce oscillations across a wide frequency band. A lack of plasma stability may also lead to a dramatic change in configuration often referred to as an explosion (and hence exploding double layer). In one example, the region enclosed in the double layer rapidly expands and evolves.^[38] An explosion of this type was first discovered in mercury rectifiers used in high-power direct-current transmission lines, where the voltage drop across the device was seen to increase by several orders of magnitude. Double layers may also drift, usually in the direction of the emitted electron beam, and in this respect are natural analogues to the smooth bore magnetron.^[39]) (not to be confused with a unit of magnetic moment, the Bohr magnetron, which is created by the “classical circular motion” of an electron around a proton).

Location Typical Voltage drop Source Ionosphere 102– 104V Satellite Solar 109– 1011V Estimated[40] Neutron star 1015V Estimated[41] Galactic filament 1017V Estimated[36] Typical Double Layers

• Magnetised plasmas: Double layers can both form in unmagnetised and magnetised plasmas.
• Cellular nature: While double layers are relatively thin, they will spread over the entire cross surface of a laboratory container. Likewise where adjacent plasma regions have different properties, double layers will form and tend to cellularise the different regions.^[42]
• Energy transfer: Double layers fascilitate the transfer of electrical energy into kinetic energy, dW/dt=I.ΔV where I is the electric current dissipating energy into a double layer with a voltage drop of ΔV. Alfvén points out that the current may well consist exclusively of low-energy particles.^[43] Torvén et al. also report that plasma may spontaneously transfer magnetically stored energy into kinetic energy by electric double layers.^[44]
• Oblique double layer: An oblique double layer has its electric field not parallel to the background magnetic field (i.e. it is not field-aligned).
• Simulation: Double layers may be modelled using kinetic computer models like particle-in-cell (PIC) simulations. In some cases it is reasonable to treat the plasma as essentially one- or two-dimensional to reduce the computational cost of a simulation.
• Bohm Criterion: A double layer cannot exist under all circumstances. In order to achieve that the electric field vanishes at the boundaries of the double layer, an existence criterion says that there is a maximum to the temperature of the ambient plasma. This is the so-called Bohm criterion.^[45] (A mathematical description is given in the math section)
• Bio-physical analogy: A model of plasma double layers has been used to investigate their applicability to understanding ion transport across biological cell membranes.^[46] Brazilian researchers have note that “Concepts like charge neutrality, Debye length, and double layer are very useful to explain the electrical properties of a cellular membrane.”.^[47] Plasma physicist Hannes Alfvén also noted that association of double layers with cellular structure,^[48] as had Irving Langmuir before him, who coined the named “plasma” after its resemblance to blood cells.^[49]

History of double layers

The research of these objects is a relatively young phenomenon. Although it was already known in the 1920s that a plasma has a limited capacity for current maintenance Irving Langmuir.^[50] He characterized double layers in the laboratory and called these structures double-sheaths. It was not until the 1950s that a thorough study of double layers started in the laboratory (e.g. Schönhuber, 1958)^{[Citation needed]}. At the moment many groups are working on this topic theoretically, experimentally and numerically.
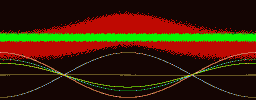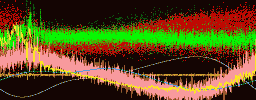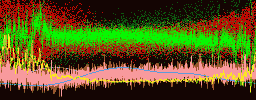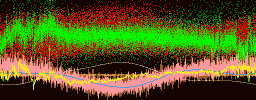
It was first proposed by Hannes Alfvén (the developer of magnetohydrodynamics) that the creation of the polar lights or Aurora Borealis is created by accelerated electrons in the magnetosphere of the Earth.^[51] He supposed that the electrons were accelerated electrostatically by an electric field localized in a small volume bounded by two charged regions. This so-called double layer would accelerate electrons Earthwards. Many experiments with rockets and satellites have been performed to investigate the magnetosphere and acceleration regions. The first indication for the existence of electric field aligned along the magnetic field (or double layers) in the magnetosphere was by a rocket experiment by McIlwain (1960). Later, in 1977, Forrest Mozer reported that satellites had detected the signature of double layers (which he called electrostatic shocks) in the magnetosphere.^[52]

The most definite proof of these structures was obtained by the Viking satellite,^[53] which measures the differential potential structures in the magnetosphere with probes mounted on 40 m long booms. These probes can measure the local particle density and the potential difference between two points 80m apart. Asymmetric potential structures with respect to 0 V were measured, which means that the structure has a net potential and can be regarded as a double layer. The particle densities measured in such structures can be a los as 33% of the background density. The structures usually have an extent of 100 m (a few tens of Debye lengths). The filling factor of the lower magnetosphere with such solitary structures is about 10%. If one out of 5 such structures has a net potential drop of 1 V then the total potential drop over a region of 5000 km would be more than the 1 kV which is needed for the electrons to create the aurora. Magnetospheric double layers typically have a strength \(e\phi_{DL}/k_B T_e \approx 0.1\) (where the electron temperature is assumed to lie in the range (\(2 eV \leq k_B T_e \leq 20 eV\)) and are therefore weak.
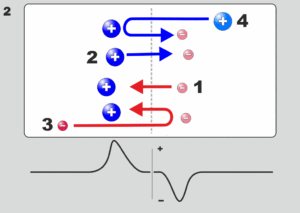
In the laboratory double layers can be created in different devices. The are investigated in double plasma machines, triple plasma machines and Q-machines. The stationary potential structures which can be measured in these machines agree very well with what one would expect theoretically. An example of a laboratory double layer can be seen in the figure below, taken from Torvén and Linberg (1980), where we can see how well-defined and confined the potential drop of a double layer in a double plasma machine is.
On of the interesting things of the experiment by Torvén and Lindberg (1980)^[54] is that not only did the measure the potential structure in the double plasma machine but they also found high-frequency fluctuating electric fields at the high-potential side of the double layer (also shown in the figure). These fluctuations are probably due to a beam-plasma interaction outside the double layer which excites plasma turbulence. Their observations are consistent with experiments on electromagnetic radiation emitted by double layers in a double plasma machine by Volwerk (1993),^[55] who, however, also observed radiation from the double layer itself. The power of these fluctuations has a maximum around the plasma frequency of the ambient plasma.

A recent development in double layer experiments is the investigation of so-called stairstep double layers. It has been observed that a potential drop in a plasma column can be split up into different parts. Transitions from a single double layer into two, three or more-step double layers are strongly sensitive to the boundary conditions of the plasma (Hershkowitz, 1992)^{[Citation needed]}. These experiments can give us information about the formation of the magnetospheric double layers and their possible role in creating the aurora.

Some scientists have subsequently suggested a role of double layers in solar flares^[56][57][58]

Mathematical description of a double layer.

In this section we will take a closer look at the mathematics behind double layers. We first describe a semi-quantitative criterion for the formation of a density dip. We then describe a particularly simple kind of double layer. We then explain how to use the distribution function and the Vlasov-Poisson equation to model more complex double layers.

Formation of a density dip.

First we will take a look at the generation of a double layer in a current carrying plasma. In 1968 Alfvén and Carlqvist showed that a density dip in a current carrying plasma can be favourable for the generation of a double layer. In this case we look at the plasma as a combination of two fluids, the moving electron fluid and the immobile ion fluid which acts as a neutralizing background. The electron fluid is treated as an essentially zero temperature beam and the ions are assumed to be collisional, and possess some finite temperature.
The density dip in the plasma (of both electrons and ions) will cause an electric field to be generated in order to keep the current density at the same level, i.e. electrons are accelerated in the decreasing part into the dip and decelerated in the increasing part out of the dip. However, this electric field will also have an influence on the first as immobile assumed ions. These ions will be driven out of the density dip, increasing it, and thereby increasing the electric field. When all ions are gone, the electric field has reached its maximum value over the dip. Note that we then have a double-double layer (increasing and decreasing electric field), and one side needs to be transported away.

We will use the quasi-static, non-relativistic description of this mechanism, which is governed by the continuity equation and the momentum equation:

\(\frac{\partial}{\partial x} (n_e v_e) = 0\)

\(m_e v_e \gt\frac{\partial v_e}{\partial x} = – e E\)

Combining these two equations we get an expression for the electric field dependent on the electron density:
\(E = – \frac{\partial}{\partial x} \left(\frac{m_e j_e^2}{2 n_e^2e^3}\right)\)
where \(j_e = -n_e e v_e\) the electron current density. The ions will experience an outward force due to this electric field, with
\(F = e n_i E = – \frac{\partial}{\partial x}(m_e n_e v_e^2)\).
Only when the force of the electric field can overcome the force by the ion pressure gradient can the evacuation of the density dip take place. Comparing the two forces (pressure and electric) assuming a quasi-neutral, thermal plasma shows after integration that this can only happen when \(k_B T_i \lt m_e v_e^2\). This happens to be the Bohm criterion for the stability of a double layer (more below).

Current carrying double layers formed by single, zero temperature beams.

We consider how a single zero-temperature beam of ions and a single zero-temperature beam of electrons, together with a trapped, zero velocity ion component, and a trapped, zero velocity electron component, may form a particular class of double layer. The trapped components are referred to as the ‘ambient plasma’ and will later be allowed to have finite temperature.

We use Poisson‘s equation and the conservation of momentum and number density to analyse the structure of these double layers, in the 1D, time-independent limit. We are looking for double layer like solutions, where there is a well localised region with a potential gradient, outside of which the electric field is zero. The region can be divided into the interval inside the double layer, where there is only one ion component and one electron component, but there is a finite field, and the outside region, where the electric field is zero. For the moment, we need only consider the inside region and the densities and velocities associated with the beams inside the layer.

The electron beam component is streaming with positive velocity \( v_{e}(x) \) (to the right), and the ion beam is streaming with negative velocity \( v_{i}(x) \) (to the left). Here, the conservation of particle energy means that \( v_{\alpha}^2(x)/2 m + q_{\alpha} \phi(x) \) is a constant, and the conservation of particle number means that the current \( j_{\alpha} = q n_{\alpha}(x) v_{\alpha}(x) \) is also a constant.

\(
|v_{\alpha}(\phi_{\alpha})| = \sqrt{v_{\alpha,0}^2 + \frac{2 e \phi_{\alpha}}{m_{\alpha}}},
\)

\(
n_{\alpha}(\phi_{\alpha}) = n_0 v_{\alpha,0} v_{\alpha}^{-1}(\phi_{\alpha})
\)

where \(\phi_e = \phi\) and \(\phi_i = \phi_{DL}-\phi\). Here \(n_0\) and \(v_{\alpha,0}\) are respectively the electron (and ion) density and particle drift speed at the low (high) potential side of the double layer.

Now we use Poisson’s equation to obtain the maximal current through the double layer, as a function of the potential drop, the fraction of current carried by the ions as compared to the electrons and a temperature limit for the ambient plasma. We chose \(\phi(x=0) = 0\) and \(\phi(x=d) = \phi_{DL}\), with \(d\) the thickness of the double layer.

\(
\rho_e = \frac{j_e}{v_e},
\rho_i = \frac{j_i}{v_i}.
\)

Thus we can write Poisson’s equation in the region inside the double layer as:

\(
– \frac{1}{4 \pi} \frac{\partial^2 \phi}{\partial x^2} = \frac{j_i}{ \sqrt{ v_{i,0}^2 + 2 e (\phi_{DL}-\phi)/m_i } } – \frac{j_e}{ \sqrt{v_{e,0}^2 + 2 e \phi / m_e } }.
\)

Introducing an integration factor \(d\phi/dx\) at both sides and integrating over \(x\) at the left hand side and over \(\phi\) on the right hand side the first integration leads to the square of the electric field \((d\phi/dx)^2\). The assumption that there is no electric field outside the double layer then leads to the ‘’Langmuir condition’’ for non-relativistic double layers:

\(
\frac{j_e}{j_i} = \frac{m_i}{m_e}.
\)

For this double layer (in a hydrogen plasma) the electron current dominates the ion current by a factor of \(\sqrt{1836}\). (Note that for the same theory for ultra-relativistic double layers gives this fraction equal to 1). Further integration, as done by Raadu (1989), then leads to the Langmuir-Child relation:

\(
j d^2 = (j_e + j_i) d^2 = \left( 1 + \sqrt{\frac{m_e}{m_i}}\right) \frac{C_0}{9} \sqrt{\frac{2e}{m_e}} \phi_{DL}^{1.5},
\)

where \(C_0\) is expressed in terms of the elliptical integrals E and K:

\(
C_0 = 2^{-1.5} (2 \sqrt{2} E ( \sin \pi / 8 ) – (1 + 2 \sqrt{2} K ( \sin \pi / 8 ) )^2 \approx 1.86518.
\)

If we now allow the ambient plasma to be at finite temperature we have to take into account reflected particles more carefully and examine how far they can penetrate into the repulsive electric field. We describe the ambient plasma by a Boltzmann distribution over the double layer:

\(
n_{\alpha,R} = n_{\alpha,0} e^{ – \frac{ e \phi_{\alpha} }{ k_B T_{\alpha} } }
\)

The densities of the reflected particles are now added to Poisson’s equation. In order that the particles in the ‘ambient plasma’ be truly trapped we require that their temperature be lower than the double layer potential. This can be seen in terms of the restriction that the potential and the electric field have to vanish at the boundaries of the double layer. The precise condition is known as the ‘’Bohm criterion’’:

\(
m_e v_e^2 \gt k_B T_i.
\)

A double layer of this type cannot form if this criterion is not met. This is the same condition under which a double layer can be formed by an ion density dip (or equivalently, for instability to parallel wavemodes like the ion acoustic or Buneman instability) as discussed before.

The Vlasov-Poisson equation.

In general the plasma distributions near a double layer are necessarily strongly non-Maxwellian, and therefore inaccessible to fluid models. In order to analyse double layers in full generality, the plasma must be described using the particle distribution function \(f_{\alpha}(\vec{x},t;\vec{v})\), which describes the number of particles of species \(\alpha\) having approximately the velocity\(\vec{v}\) near the place \(\vec{x}\) and time \(t\).

The Vlasov-Poisson equations give the time-dependent interaction of a plasma (described using the particle distribution) with its self-consistent electric field. The Vlasov-Poisson equations are a combination of the Vlasov equations for each species \(\alpha\) (also called the collisionless Boltzmann equation (CBE). We take the nonrelativistic zero-magnetic field limit);

\(
\frac{\partial}{\partial t} f_{\alpha} + \vec{v} \cdot \frac{\partial}{\partial \vec{x}} f_{\alpha} + \frac{q_{\alpha}\vec{E}}{m_{\alpha}} \cdot \frac{\partial}{\partial \vec{v}} f_{\alpha} = 0, \)

and Poisson’s equation:

\(
\nabla \cdot \vec{E} = – \frac{\partial^2\phi}{\partial x^2} = 4 \pi \rho.
\)

Here \(q_{\alpha}\) is the particle’s electric charge, \(m_{\alpha}\) is the particle’s mass, \(\vec{E}(\vec{x}, t)\) is the electric field, \(\phi(\vec{x}, t)\) the electric potential and \(\rho\) is the electric charge density.

Footnotes

External links

• A double layer review (1978), L.P. Block
• Electrostatic double layers and a plasma evacuation process (1981), Raadu, M. A.; Carlqvist, P.
• On the physics of relativistic double layers (1982), Per Carlqvist
• On the role of double layers in astrophysical plasmas (1985), Smith, R. A.
• Double Layers in Astrophysics (1987) Proceedings of Workshop held in Huntsville, Ala., 17-19 Mar. 1986 sponsored by NASA, Washington and USRA. (Contents) (NASA Record) Full text PDF
• Dynamical aspects of electrostatic double layers (1988) M. A. Raadu, & J. J. Rasmussen
• Filamentary Double Layers (PDF, 1993), W.L. Theisen, R.T.Carpenter, R.L.Merlino
• Energy release in double layers (1985), Raadu, M. A.
• Parallel electric fields accelerating ions and electrons in the same direction (1988), Hultqvist, Bengt; Lundin, Rickard
• Parallel electric fields in the upward current region of the aurora: Numerical solutions (2002, PDF), R.W. Ergun, et al.
• Numerical modeling of low-pressure plasmas: applications to electric double layers (2006, PDF), A. Meige, PhD thesis

References

• Alfvén, H., On the theory of magnetic storms and aurorae, Tellus, 10, 104,. 1958.
• Peratt, A., Physics of the Plasma Universe, 1991
• Raadu, M.,A., The physics of double layers and their role in astrophysics, Physics Reports, 178, 25 – 97, 1989.